Approximating Decision-TSP with ML and Heuristics

Feb 24, 24

When tackling NP-hard problems like the Traveling Salesman Problem (TSP), exact solutions quickly become infeasible for larger graphs. Instead, heuristics and machine learning can provide approximate but effective answers. In our university project Decision-TSP (GitHub repo), we explored how to combine heuristic algorithms with regression models to predict whether a Hamiltonian cycle shorter than a given threshold exists.

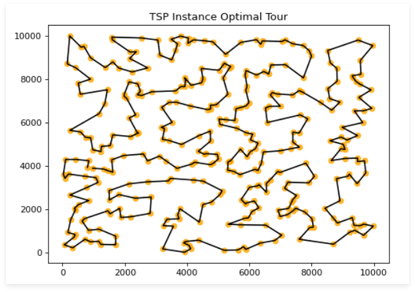
The Problem Setup

We framed TSP as a decision problem:

  • Input: A complete weighted graph with nodes represented by 2D coordinates, edge weights calculated using the Euclidean distance, and a length bound n.
  • Output: A binary decision — does there exist a tour shorter than n?

Our datasets consisted of 1,000–2,000 instances with 300–600 nodes each, including both evenly distributed and clustered graphs.

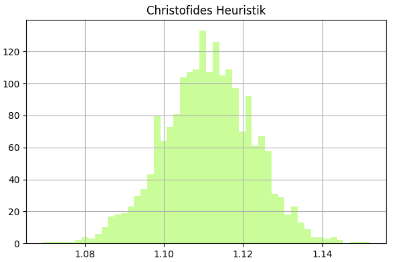
drawing

Heuristics as Features

Instead of directly computing optimal solutions, we derived nine heuristics (including 2 lower bounds and 7 approximations). These heuristics provided a fast estimate of tour lengths while avoiding exponential runtimes.

The heuristics were carefully modularized in heuristics_pipeline.ipynb, ensuring reusability and clear benchmarking across datasets.

A key coding practice here was clean separation of heuristics into functions, making it easy to test, extend, and evaluate new strategies.

drawing

Data Generation with Multi-Threading

Working with thousands of TSP instances required large-scale data generation. To avoid bottlenecks, we used Python’s multi-threading to parallelize the computation of heuristics.

This drastically reduced preprocessing time, transforming what would have been hours of sequential execution into manageable runtimes. For large-scale ML experiments, this optimization was critical.

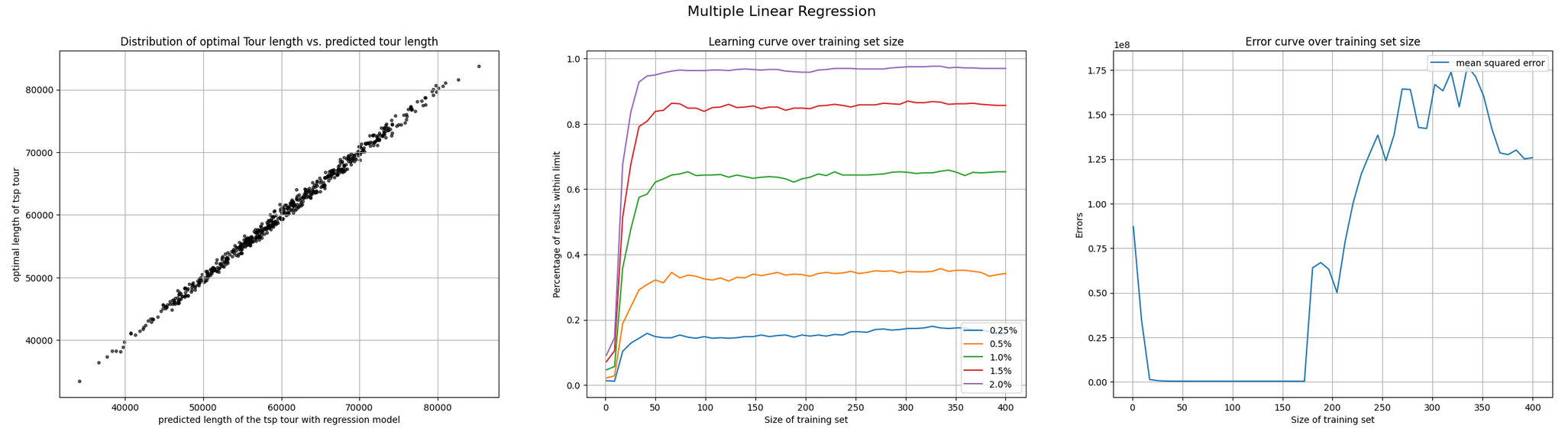
Regression Models for Prediction

We then trained several regression models using heuristics as input features and the optimal tour length as the target:

  • Multiple Linear Regression (MLR)
  • Decision Tree Regressors
  • Support Vector Regression (SVR)
  • Neural Networks

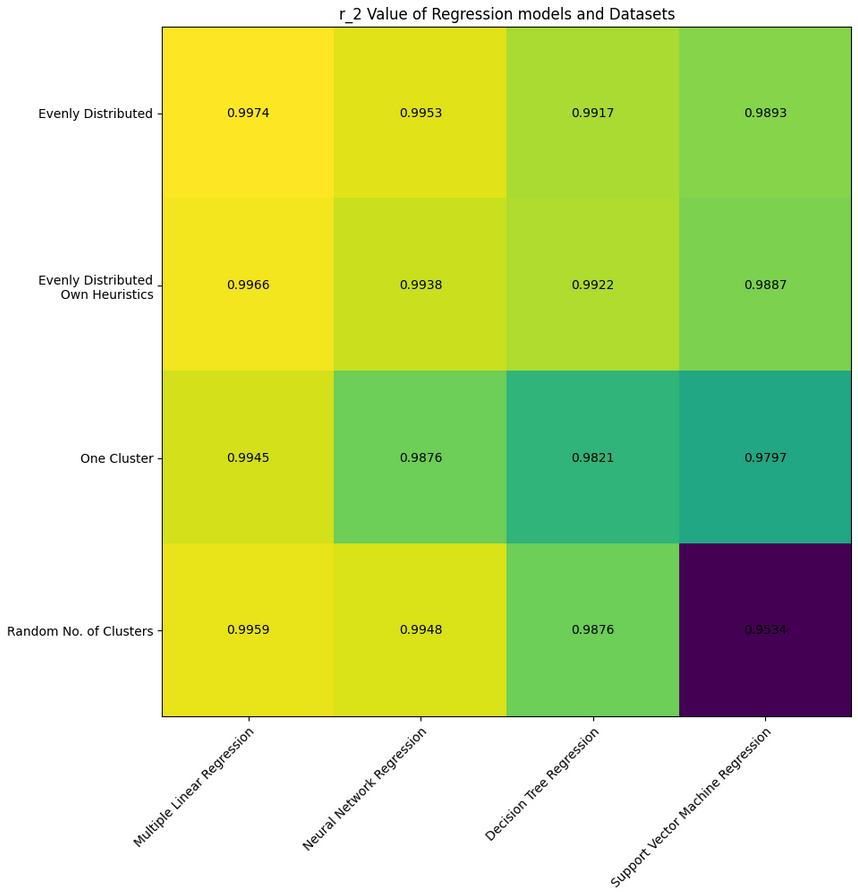
Among these, MLR achieved the best trade-off between accuracy and simplicity, with R² values exceeding 0.99 across datasets. This demonstrated that simple models can outperform more complex methods when combined with strong heuristic inputs.

drawing drawing

Key Takeaways

  • Heuristics matter: heuristics computable in polynomial time generate real insight in approximating NP-hard problems.
  • Efficient coding practices: Clear modularization and multi-threaded data generation saved significant time and made experiments scalable.
  • MLR wins: While neural networks and SVRs are powerful, Multiple Linear Regression proved the most reliable for Decision-TSP, showing how classical ML techniques can shine in structured optimization problems.

This project showed us how combining heuristics with lightweight ML models can bring both accuracy and efficiency to NP-hard problems. The coding optimizations especially in heuristics implementation and threading were just as important as the theoretical models themselves.

Resources